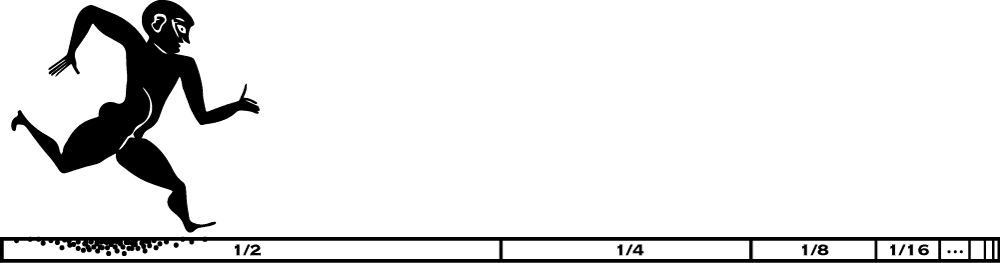
Figura 1: Corrida de Aquiles, a qual só possui um fim após um número infinito de etapas

Zenão de Eleia é estimado de ter nascido por volta de 490 BCE (Before Commom Era) e quase tudo que se sabe sobre ele, está escrito nas páginas iniciais do livro de Platão, “Parmenides”.
Zenão foi um filósofo responsável por escrever um livro onde existiam 40 paradoxos lógicos. Infelizmente o livro original foi há muito perdido, e os únicos fragmentos encontrados são obtidos através de outros filósofos parafraseando Zenão.
Um de seus mais famosos Paradoxos é o da Dicotomia, onde supomos que o corredor Aquiles começa uma corrida e depois de um certo tempo, corre ½ do trajeto total, então corre mais ¼ do caminho, mais ⅛, e continua o caminho até o infinito, nunca alcançando o fim da corrida.

Figura 2: Animação mostrando trajeto de Aquiles.

Zenão, pelo menos como retratado pela Física Aristotélica, argumentou que, como consequência deste paradoxo, o movimento não existe. Uma vez que um número infinito de etapas não pode ser concluído, Aquiles nunca alcançará a linha de chegada.
Este paradoxo ficou por muito tempo na gaveta dos filósofos, sem explicações racionais e coerentes.
No entanto, a matemática moderna fornece agora, maneiras de explicar como Aquiles pode completar a corrida. Como Salmon (1998) apontou, grande parte do mistério da caminhada de Zenão é dissolvida dada a definição moderna de um limite. Isso fornece um sentido preciso em que a seguinte soma converge:

1/2 + 1/4 + 1/8 + 1/16 + …

Embora esta soma possua infinitos elementos, ela é uma série geométrica que converge para 1, na topologia padrão dos números reais, e portanto, Aquiles seria capaz de finalizar a corrida, matematicamente falando.

Referências:

Salmon, W. A Contemporary Look at Zeno’s Paradoxes: An Excerpt from Space, Time and Motion, in Metaphysics: The Big Questions, van Inwagen and Zimmerman (Eds.), 1998, Malden, MA: Blackwell Publishers Ltd.

Black, M., 1951, Achilles and the Tortoise, Analysis, 11(5): 91–101.