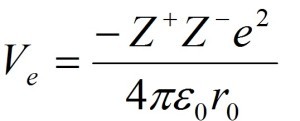A estrutura perovskita é conhecida e estudada a mais de um século, desde a descoberta do mineral CaTiO3 por Gustav Rouse em 1839. A estrutura foi batizada com esse nome em homenagem ao mineralogista russo Count Lev Alexevich von Perovski. Desde então, o nome perovskita é usado para nomear uma classe de materiais que têm formula química do tipo ABC3, na qual os íons do sítio B são coordenados (rodeados) por um octaedro de íons do sítio C. Uma subclasse bastante conhecida da família das perovskitas, nos dias atuais, são os compostos com a formula química ABO3, em que os cátions do sítio B são metais de transição e os íons do sítio C são oxigênios.
A estrutura perovskita pode ser encontrada com algumas simetrias de rede, tais como cúbica, tetragonal, ortorrômbica, romboédrica ou monoclínica. A estabilidade simétrica dessa estrutura é bastante frágil e depende de uma série de fatores. As forças físicas que atuam nos íons da estrutura perovskita, e que são responsáveis pela estabilidade estrutural, não são claramente conhecidas. De fato, “um completo e compreensivo tratamento das forças físicas” por trás das distorções estruturais que ocorrem na estrutura perovskita “nunca foi publicado na literatura”. No entanto, um fato conhecido nesse processo é que os octaedros de oxigênio que existem na estrutura perovskita se “inclinam ou giram” para reduzir a energia total do sistema. O entendimento exato de como isso ocorre não é de fácil compreensão e pode variar de caso a caso. As forças que atuam nesse sistema são muitas e na maioria das vezes competem entre si para estabilizar uma dada simetria. Assim, um delicado balanço entre essas forças determina a simetria de menor energia. A energia relacionada com uma mudança de simetria é bastante baixa (para alguns casos da ordem de alguns décimos de eV) e o balanço de forças pode ser mudado simplesmente com a variação de alguns poucos graus de temperatura. Várias abordagens são utilizadas para tentar entender esses fenômenos, como exemplo: correlações empíricas focando os tamanhos de íons, o número de coordenação e várias considerações geométricas; cálculos de energia total de rede por modelos empíricos; cálculos da energia de banda usando várias aproximações. Cada uma dessas abordagens tem seus pontos fracos e fortes, e cada uma oferece uma perspectiva diferente sobre o problema.
Apesar da limitação na compreensão do arcabouço de forças envolvidas nas estruturas perovskita, alguns avanços já foram alcançados na tentativa de compreendê-las. Na simetria de rede cúbica (grupo espacial Pm3m), por exemplo, sabe-se que o cátion metálico do sítio A possui número de coordenação 12, ou seja, ele é cercado por 12 oxigênios como primeiros vizinhos. Além disso, ele pode ser monovalente, bivalente ou trivalente, dependendo do átomo em questão. O cátion do sítio B, comumente um metal de transição, se localiza no centro da estrutura de oxigênios e possui número de coordenação 6. A simetria cúbica, em geral, se estabiliza em mais altas temperaturas que as demais simetrias. No entanto, a maioria das demais simetrias deriva da simetria cúbica (com a diminuição da temperatura) por meio de pequenos deslocamentos de seus íons.
Para se acomodar em estados de menor energia, as estruturas perovskita podem sofrer vários tipos de distorções envolvendo os átomos que a compõem. As mais importantes são aquelas envolvendo: (a) os deslocamentos iônicos, no qual os íons dos sítios A e B se deslocam para fora de sua de sua posição de equilíbrio na cela cúbica; (b) as rotações ou inclinações dos octaedros “BO3”; e ambas as distorções, inclinações e deslocamentos.
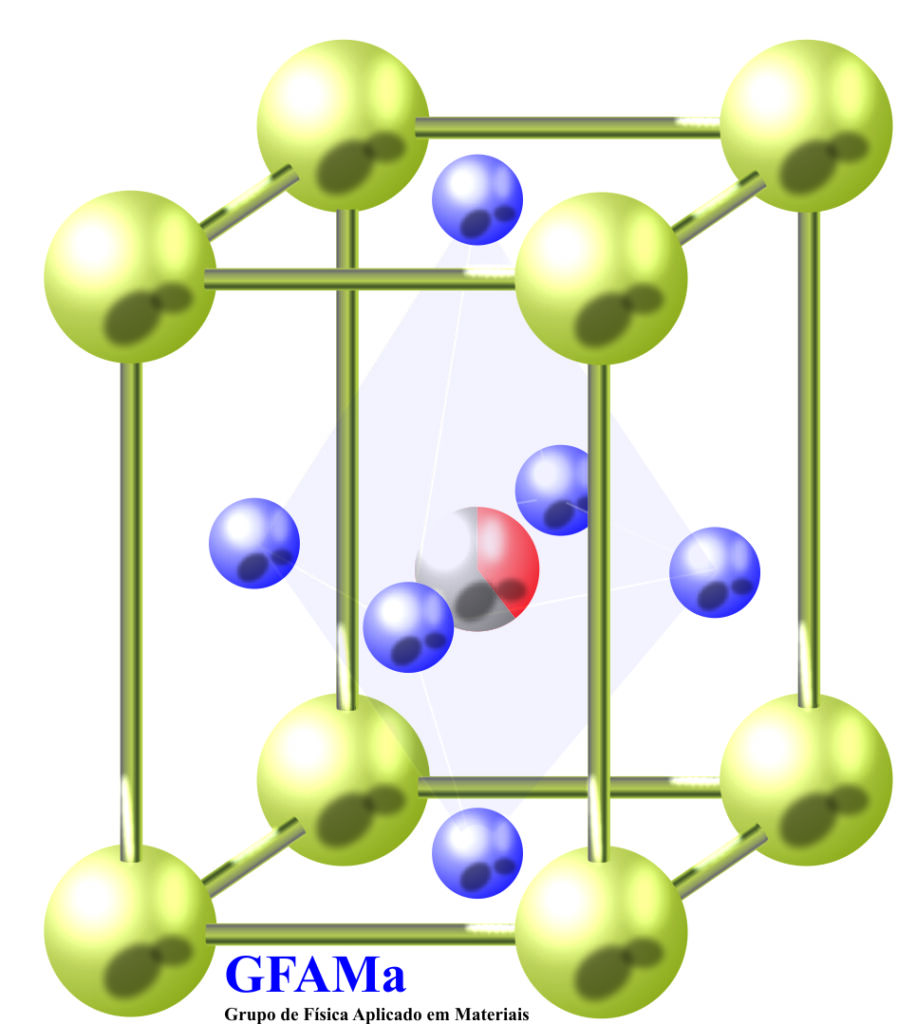
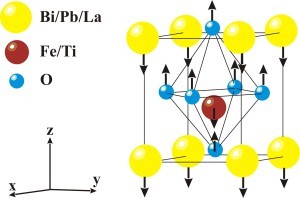
(a) A transição da simetria cúbica para a tetragonal, por exemplo, é alcançada por uma transição de fase displaciva, pela qual a mudança de simetria ocorre simplesmente por uma ligeira mudança nas posições dos átomos. Nessa transição, os cátions do sítio A e B se deslocam em uma dada direção ao passo que os ânions se deslocam em outra, como ilustra a Figura 1. Neste arranjo a estrutura perovskita muda da simetria cúbica para a tetragonal e adquire ordem ferroelétrica. A magnitude dos deslocamentos atômicos, na transição displaciva, são diferentes para diferentes íons e, com isso, a estrutura ganha um caráter polar. O deslocamento dos íons do sítio B são maiores que os do sítio A e O, também, os deslocamentos do oxigênio na direção “Z” é maior que nas direções “X” e “Y”. Por intermédio desse arranjo, uma estrutura perovskita reduz sua simetria de cúbica para tetragonal.
Figura 1. Deslocamento iônico na transição da simetria cúbica para a tetragonal. Adaptado da referência [26].
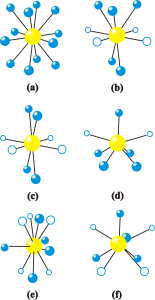
(b) Um grande número de diferentes materiais com estrutura perovskita é reportado pela literatura. A possibilidade da existência de vários materiais diferentes, com diferentes íons de diferentes tamanhos, é atribuída à inclinação ou “giro” da estrutura octaédrica de oxigênio no interior da cela unitária. Essa inclinação permite acomodar diferentes tipos de cátions metálicos com diferentes raios iônicos. Assim, as diferentes simetrias de rede, como por exemplo, as simetrias ortorrômbica, romboédrica e monoclínica, são alcançadas partindo da inclinação do octaedro de oxigênio no interior da cela unitária de simetria cúbica. O efeito geométrico que a inclinação do octaedro de oxigênios acarreta é a mudança na distância A-O e no número de coordenação do sítio A, enquanto a coordenação do sítio B pouco muda. Na estrutura com simetria cúbica existem 12 oxigênios como primeiros vizinhos dos átomos do sítio A, porém, quando a estrutura octaédrica de oxigênios se inclina a vizinhança diminui e, para alguns casos, pode se tornar 7 o número de primeiros vizinhos. A Figura 2 ilustra algumas das possíveis inclinações e consequentes coordenações dos átomos do sítio A, segundo a notação de Glazer para as inclinações. Nessa notação, “a”, “b” e “c” são os eixos de rotação, “+” e “-” especificam o sentido de rotação com relação a camada adjacente e, se não houver rotações, é especificado por “0”. Esse mecanismo encontra-se melhor detalhado na referencia [1].
Figura 2. Coordenação (n°) do sítio A nas estruturas perovskitas do tipo ABO3 ocasionadas por diferentes inclinações do octaedro de oxigênios. As diferentes figuras correspondem às inclinações (a) a0a0a0 (23), n° 12, (b) a0a0c– (22), n° 8, (c) a0a0c+ (21), n° 8, (d) a0b–b– (20) , n° 7, (e) a–a–a– (14) , n° 9, (f) a+a–a– (11) , n° 8. Os círculos maiores (amarelos) são os cátions do sítio A, os círculos menores (azuis) e fechados os primeiros ânions vizinhos e os círculos menores abertos os segundo ânions vizinhos. Adaptado da referencia [1].
As distorções e deslocamentos, que mudam a simetria de rede da estrutura perovskita, ocorrem, mais comumente, em função da temperatura. Normalmente, acima da temperatura de transição ferroelétrica (temperatura de Curie) a estrutura se encontra na simetria cúbica e abaixo da temperatura crítica a estrutura muda para uma simetria menor (tetragonal, ortorrômbica, romboédrica ou monoclínica). Partindo da simetria cúbica, a estrutura perovskita sempre diminui sua energia livre quando ocorrem as distorções que mudam a simetria. A quantidade de energia que é diminuída quando a estrutura se distorce é pequena, da ordem de um décimo de eV. A energia adicional necessária para estabilizar uma ou outra simetria é bastante baixa e depende de uma série de fatores, como será discutido no próximo tópico. Entretanto, na maioria dos casos, as mudanças na ligação química A-O são determinantes para estabilizar uma determinada simetria. Os deslocamentos espontâneos dos átomos, que ocasionam as mudanças de simetria, são geralmente associados aos fônons “Soft”, que são uma vibração particular da rede cristalina, cuja frequência de vibração tende a zero próximo a temperatura de Curie (TC). Conceitualmente, é possível interpretar os deslocamentos vibracionais dos íons no modo “soft” como se eles se congelassem quando a temperatura atinge TC. Assim, quando a temperatura é diminuída até a temperatura de Curie a vibração do modo “soft” é congelada e o deslocamento dos íons ocorre espontaneamente.
Apesar de não haver um completo entendimento a cerca das forças por trás da estabilidade estrutural nas estruturas perovskitas, alguns avanços são encontrados em trabalhos atuais da área, que surgem no sentido de descrever esses sistemas [2,3,20]. Na ausência de uma clara interpretação, na qual as quantificações matemáticas seriam suplementadas pelas argumentações físico-químicas, a natureza das interações que estabilizam a estrutura pode ser analisada de alguns pontos de vista diferentes, mas, infelizmente, não complementares. Entre eles, dois pontos de vista são tidos como relevantes: o ponto de vista físico e o químico.
Do ponto de vista físico, as forças físicas responsáveis pelas interações entre íons são bastante complexas e envolvem interações de múltiplos corpos, as quais são praticamente impossíveis de serem descritas analiticamente. No entanto, algumas aproximações podem ser usadas para descrever tal sistema, como é o caso do potencial de Madelung e do cálculo de energia descrito pela equação de Born-Landé.
O potencial de Madelung é definido como o potencial eletrostático que um íon sente devido a todos os outros íons. O íon do sítio B, como exemplo, é rodeado por íons de oxigênio carregados negativamente e íons do sítio A carregados positivamente. Os elétrons orbitando o íon do sítio B experimentam um potencial eletrostático repulsivo (Potencial de Madelung), devido aos íons do sítio A e atrativo devido aos íons do sítio de oxigênio [26]. Max Born e Alfred Landé propuseram, em 1918, que a energia da rede (forças de longo alcance) poderia ser calculada por meio do potencial eletrostático (potencial de Madelung) e de um potencial de repulsão (forças de curto alcance). As forças de longo alcance, ou forças de Coulomb (que favorecem as estruturas distorcidas), são referentes ao campo eletrostático sentido por cada íon da estrutura, gerado pelas cargas elétricas dos demais íons [[vi]]. O potencial eletrostático “Ve” pode ser descrito, de uma forma geral, pela equação:
Sendo, “Z+” o número de cargas catiônicas, “Z–” o número de cargas dos ânions, “e” a carga elétrica elementar, “e0” a permissividade elétrica no vácuo e “r0” a distância entre os íons.
As forças repulsivas de curto alcance (que favorecem a estrutura com simetria cúbica) são referentes às interações diretas entre pares de íons e estão relacionadas com as repulsões de Pauli a curtas distâncias. O potencial descrito por Born para descrever a interação repulsiva entre íons pode ser descrito pela seguinte equação:
Vr = B/r^n
Sendo, “B” uma constante, “r” a distância entre íons e “n” um número entre 5 e 12. Assim, do ponto de vista físico, ambas as forças competem para estabilizar a estrutura, sendo que as repulsões de curto alcance favorecem a estabilidade da simetria cúbica e as forças de longo alcance favorecem a estabilidade das simetrias mais baixas .
Do ponto de vista químico, as ligações químicas podem se utilizadas para discutir a estabilidade estrutural que envolve as estruturas perovskita. Nesse sentido, as ligações químicas na estrutura perovskita deveriam ter um caráter iônico forte, o que estabilizaria a estrutura nas mais altas simetrias, como a cúbica. No entanto, dependendo dos íons que formam a estrutura o caráter das ligações pode covalente, o que acarreta as conhecidas distorções ferroelétricas e as simetrias de rede tetragonal, romboedral, ortorrômbico ou monoclínico.
A origem das distorções experimentadas pela simetria cúbica, e que geram as simetrias tetragonal ou romboedral, foi discutida por Cohen que comparou os compostos BaTiO3 (ferroelétrico fraco) e PbTiO3 (ferroelétrico forte). Por intermédio dos estudos de densidade de estados eletrônicos foi demonstrado que os estados Ti(3d) são fortemente hibridizados com os estados O(2p) em ambos os materiais (ligações B-O) e que essa hibridização é reforçada pela distorção estrutural. Também foi demonstrado que as ligações entre Pb(6s) e O(2p) são fortemente hibridizadas e que as ligações Ba(5p) e O(2p) têm um caráter fortemente iônico. Ou seja, o composto PbTiO3 possui a ligação A-O hibridizadas, consequentemente, sua estrutura é mais distorcida e sua ordem ferroelétrica é intensificada quando comparada com a ordem no BaTiO3. Os fenômenos decorrentes desse processo são todos relacionados com os íons que compõe o sítio A. De fato, quando o íon do sítio A possui uma determinada configuração eletrônica, envolvendo os orbitais “s” e “p”, ele se liga ao íon de oxigênio por uma ligação hibridizada, na qual os orbitais se sobrepõem e assumem uma configuração intermediária de energia. Essas ligações hibridizadas diminuem a distância entre os íons e confere um caráter covalente a ligação. Além disso, a hibridização da ligação A-O interfere, indiretamente, na ligação B-O, visto que os compostos no qual a ligação A-O não é hibridizada (BaTiO3) possuem a ligações B-O enfraquecidas.
Outro fator do ponto de vista químico, que deve ser relevante para a distorção da estrutura perovskita perfeitamente simétrica (cúbica-não ferroelétrica) para uma estrutura menos simétrica (tetragonal, romboedral, ortorrômbica ou monoclínica-ferroelétrica) é a formação dos pares de elétrons solitários, do inglês “Lone Pairs”. Os “Lone Pairs” são considerados pares de elétrons quimicamente inertes, os quais são ligados entre si, porém não participam das ligações químicas entre íons. A principal atuação na estrutura desses elétrons seria produzir uma “pressão química” que seria responsável por distorcer a estrutura perovskita e ocasionar a ferroeletricidade. Apesar dos estudos sobre os pares de elétrons serem ainda bastante recentes, e os estudos acerca da sua natureza e origem ainda não serem conclusivos, a atuação deles na distorção estrutural já é bem aceita pela comunidade científica da área. Essa origem, dos pares de elétrons solitários, foi investigada no óxido de chumbo (PbO). A investigação indicou que o “Lone Pairs” é um resultado direto da interação cátion – ânion. Os autores acreditam que os pares de elétrons solitarios são ativados por meio da interação dos estados antiligantes da ligação Pb(6s) – O(2p) com o orbital não preenchido do Pb(6p). A natureza e os detalhes de tal interação ainda são controversos, e não serão abordados no presente trabalho.
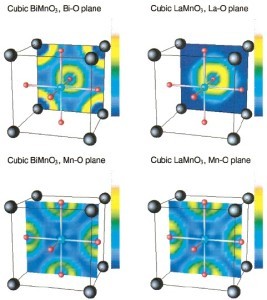
Em um estudo recente realizado por Seshadri e colaboradores,o papel dos “Lone Pairs” na distorção ferroelétrica dos compostos BiMnO3 e LaMnO3 foi investigado com o uso de uma função de localização de elétrons (ELF) em cálculos de primeiros princípios. Os resultados dessa investigação são apresentados na simulação da estrutura cúbica ilustrada na Figura 3. Os íons dos vértices da estrutura perovskita (azul escuro) são: à esquerda Bi e a direita La; Os íons do centro da estrutura (azul claro) são Mn; Os íons das faces da estrutura (vermelho) são os oxigênios. A análise foi realizada em dois planos, no plano A-O e no Mn-O. As localizações eletrônicas no plano Mn-O são muito similares para ambos os compostos. A grande diferença ocorre para as localizações eletrônicas no plano A-O. Os “Lone Pairs” ativos no Bi(6s) são esfericamente distribuídos (anéis amarelos) ao redor do átomo de Bi na estrutura com simetria cúbica. No entanto, a cor azulada ao redor dos átomos de La indica que os elétrons não são localizados nessa região. A forma esférica desses “Lone Pairs” (em torno dos átomos de Bi), ilustrada aqui em uma simulação com a simetria cúbica, não é estável a baixas temperaturas. Abaixo de “TC” eles têm a tendência a adquirirem um formato oval (lobo) o qual distorce a estrutura e a conduz para as estruturas de mais baixa simetria (tetragonal, romboedral, ortorrômbica ou monoclínica) com caráter polar, nas quais as propriedades ferroelétricas são observadas.
Figura 3. Valência eletrônica projetada em dois planos atômicos [(100) e (200)] da estrutura perovskita. As cores representam a localização eletrônica, regiões com elétrons menos localizados “azul” e mais localizados “Amarelo”. Retirado da referência [1].
Os estudos apresentados acima não são inteiramente conclusivos sobre a natureza física e química das interações entre íons, responsáveis por estabilizarem uma determinada simetria de rede. No entanto, o arranjo apresentado acima é sempre discutido nos trabalhos da área e eles são os guias existentes usados para a compreensão da estabilidade estrutural das estruturas perovskita de interesse para o presente trabalho.
[1] Valdirlei F. Freitas, “O Composto Bifeo3-Pbtio3dopado com La: Relações Propriedade/Estrutura”, Tese confeccionada para a defesa de titulo de doutorado, Universidade Estadual de Maringá, http://www.pfi.uem.br/site/index.html, 2011.