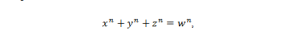Pierre Fermat viveu na França do século XVIII e era funcionário público na cidade francesa de Toulouse, a matemática para ele era um passatempo, dedicando seu tempo livre a mesma. Uma das características de Fermat que ficou famosa era o seu costume de apresentar a outros matemáticos problemas desafiantes, que muitas vezes deixavam seus contemporâneos atolados na tentativa de solucioná-los.
O seu pai, Dominique de Fermat, era um rico mercador de peles que lhe proporcionou uma educação privilegiada, inicialmente no mosteiro franciscano de Grandselve e depois na Universidade de Toulouse. Ingressou ao serviço público em 1631. Em 1652 foi promovido a Juiz Supremo, na Corte Criminal Soberana do Parlamento de Toulouse. Neste mesmo ano Fermat adoeceu e chegou a afirmar-se que tinha morrido.
Fermat desenvolveu a Geometria Analítica em 1629 e descreveu as suas ideias num trabalho não publicado intitulado Introdução aos lugares geométricos planos e sólidos, que circulou apenas na forma de manuscrito. Neste trabalho Fermat introduziu a ideia de eixos perpendiculares e descobriu as equações gerais da reta, circunferência e equações mais simples para parábolas, elipses e hipérboles, e depois demonstrou que toda equação de 1º e 2º grau pode ser reduzida a um desses tipos. Nada disto está no ensaio de Descartes, apesar deste ter tido acesso à Introdução vários meses antes de publicar a sua obra intitulada Geometria, de 1637.
Grande parte de seus feitos não foram publicados, pois Fermat dedicava-se a matemática como um passa-tempo e seus feitos foram reconhecidos após a sua morte quando seu filho no revirar as paginas dos livros que seu pai lia, encontrou diverças anotações intereçantes, comprovações de teoremas e até mesmo a criação de alguns.
O que acabou por deixar Fermat tão famoso não foi suas publicações e sim uma peculiar proposição levantada do teorema de Pitágoras que inseriu num de seus livros que estudava:
“É impossível para um cubo ser escrito como a soma de dois cubos ou uma quarta potência ser escrita como a soma de duas quartas potências ou, em geral, para qualquer número que é uma potência maior do que a segunda, ser escrito como a soma de duas potências com o mesmo expoente”. Ou seja, a igualdade jamais será satisfeita.
A questão é que Fermat deixou sua proposição sem comprovação com uma pequena nota no rodapé do livro, “Descobri uma demonstração maravilhosa desta proposição que, no entanto, não cabe nas margens deste livro”. – Mas qual seria essa demonstração? – Pergunta que assombrou os matemáticos por um longo tempo. Dos matemáticos famosos que tentaram solucionar o problema estão inclusos: Euler, Dirichlet (1828), Legendre (1830), Gabriel Lamé (1839), Sophie Germain, Kummer e mais recentemente, Wagstaff (1980). O interessante que a proposição levou a construção aprimorada da teoria dos números tal como a formulação, desconstrução e aprimoramento de toda a geometria no plano real e dos complexos para n dimensões.
– Mas a pergunta que não quer calar o leitor, é: O que isso tem a ver com a física?
Não é preciso saber-se muito sobre a Física ou sobre a Matemática, para saber que a Física é uma ciência fundamentada na Matemática, numa tentativa de descrever o Universo do qual vivemos por meio de cálculos que descrevem fenômenos naturais. Logo, com a evolução da Matemática no estudo dela mesma, propicia na criação de ferramentas que contribuem no saber cientifico. E como o teorema de Fermat é fundamentada basicamente na geometria pitagórica da qual a Física também o é, temos mais uma ferramenta que pode ajudar na derrubada de hipóteses dentro da Física Teórica, pois por muitas vezes acaba-se caindo em problemas semelhantes como em casos tensoriais ou na própria teoria dos números ou ainda, em casos mais simples de geometria. E mesmo dentro da Física por muitas vezes encontramos Euler, Lagrange e Kummer com conjurações que propiciam a Física no geral, e muitas dessas conjurações se devem ao fato, de os mesmos terem estudado o teorema de Fermat, um exemplo:
Apresentada por Euler, em que a igualdade se satisfaz. Além disso Euler apresentou uma solução para o teorema derrubando a afirmação quando considerou para n os números primos impares dizendo que havia solução, mas o problema está em encontrar os números primos, sendo uma outra hipótese para se comprovar. Mesmo com tal proposta, a proposição de Fermat se manteve.
Atualmente o teorema de Fermat possui sua demonstração, pois a mesma só foi possível após 350 anos de estudo fundamentada na geometria e nos números que levaram a diversas comprovações e teoremas aplicados nas mais diversas áreas da Física e da Matemática. A solução do teorema se deve a Andrew Wiles, um professor da Universidade de Princeton, que a partir da análise da conjectura de Taniyama-Shimura percebeu que o teorema poderia ser solucionado, mas para isso necessitava-se comprovar a conjectura, da qual o fez. Por tal feito, Wiles foi recompensado com o prêmio $50.000 libras dado pela Fundação Wolfskhel.
Apesar de tantos anos terem se passado, e o teorema ter sido demonstrado, ainda restam dúvidas a respeito da demonstração encontrada por Fermat. Pois necessitou de ferramentas construídas séculos depois de sua morte para a comprovação do mesmo. Será que existe uma demonstração mais simples? Só os próximos anos dirão.
Referencias:
CUNHA DA SILVA, Daniel – O Último teorema de Fermat, UERJ, 2010.
JACINTO, Jaime Ferreira – O Último Teorema de Fermat, FAFI União da Vitória, 2007.
SINGH, Simon – O Último Teorema de Fermat. A história do enigma que confundiu as maiores mentes do mundo durante 358 anos. Rio de Janeiro, Ed. Record, 1998.
http://www.infoescola.com/matematica/ultimo-teorema-de-fermat/ acessado no dia 28/09/2015 as 12:45h.
Autor: Maycol W. Szpunar