A geometria euclidiana sempre nos foi mais familiar e tradicionalmente é por meio desta que entendemos os conceitos básicos como: dimensão, comprimento, área e volume, aplicando-os em suas formas geométricas.
Apesar da compreensão concedida pelos conceitos citados anteriormente podemos observar que a natureza e suas formas não podem ser eficazmente explicadas por moldes da geometria euclidiana, a frase de Benoit B. Mandelbrot, dita na década de 70 ressaltava que: “As nuvens não são esferas, as montanhas não são cones, as linhas costeiras não são círculos e a casca de uma árvore não é suave, nem os relâmpagos se propagam em linha reta”. Assim supondo que a natureza apresentava uma complexidade maior do que a oferecida pela geometria euclidiana, eis que surge então a necessidade de uma teoria especial que estudasse e compreendesse tais formas complexas da natureza, essa geometria foi nomeada como geometria fractal.
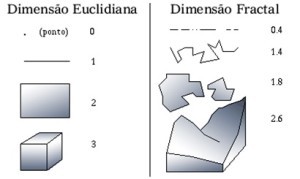
O nome fractal vem do latim “fractus” que significa fração, quebrado e que representam muito bem a nova geometria criada devido à nova concepção de dimensão, pois na pela nova geometria os objetos reais podem ser descritos com uma dimensão que não é um número inteiro. Podemos entender melhor olhando as diferenças no conceito de dimensão da geometria fractal e da geometria euclidiana pela figura 1:
Figura 1 – Comparação da dimensão euclidiana e dimensão fractal. Siqueira (2009)
Outras propriedades dessa geometria, além da sua dimensão fracionária, são a auto-semelhança, que é a capacidade do fractal de se reproduzir em uma mesma figura em diferentes escalas (geralmente decrescentes), podendo gerar, por exemplo, uma replica do todo em uma escala menor e a complexidade infinita, que se refere ao processo de formação da figura fractal ser recursiva, ou seja, pode ser gerado com uma cadeia de processos iguais, executados de maneira consecutiva e que matematicamente concede tal propriedade (para fractais ideais, pois fractais reais possuem algumas limitações de escala).
Figura 2 – Fractal Computacional (Fractal Ideial).
Figura 3 – Visão fractal de uma couve-flor (Fractal Real).
A investigação sobre o caos teve início na década de 60 e apesar de recente é considerada uma das grandes revelações para as ciências físicas. A matemática desenvolvida pela Teoria do Caos surgiu para lidar com o objetivo de compreender e dar respostas às flutuações erráticas e iregulares que se encontram na natureza.
Uma das leis do caos é em relação às condições iniciais de sistemas que evoluem com o tempo (dinâmicos). O comportamento do sistema pode tomar rumos completamente diferentes quando se tem uma modificação, por menor que seja nas suas condições iniciais.
A geometria fractal está fortemente ligada ao caos. São nas estruturas e figuras irregulares, estranhas (e de certa forma belas) que esta geometria busca encontrar padrões organizados dentro de um sistema aparentemente aleatório.
As aplicações da geometria fractal vão muito além da matemática e do tratamento de estatísticos e noções de probabilidade de dados dispersos caoticamente. As contribuições podem ser vista na da ciência natural como na biologia e o crescimento de seres microscópicos em um meio que possui quantidade de nutrientes limitados, na química com análise de superfícies para maior eficácia em reações químicas e na física trazendo novos horizontes para o estudo de entropia, que estuda o grau de desordem e complexidade de um sistema e no estudo de difusão de sistemas. Entretanto há aplicações em inúmeras áreas como na medicina (ligados ao funcionamento do coração e pulmão, sistema circulatório e análise de células cancerígenas), na economia (pelo comportamento das bolsas de valores), nas ciências sociais (com o comportamento de multidões).
Buscando ordem no caos e semelhanças presente nas coisas naturais, podemos dizer, matematicamente falando, que o que o mundo a nossa volta tem em comum é só um “número quebrado”.
Referências:
ASSIS, T. A., et al., et al. Geometria Fractal: Propriedades e Características de Fractais Ideais. Revista Brasileira de Ensino de Física. 2008, Vol. 30, p. 2304.
Costa, D. L. H. Geometria Fractal.
Backes, A. R e Bruno, O. M. Técnicas de Estimativa da Dimensão Fractal: Um Estudo Comparativo. 2005.
Costa, L. F. e Bianchi, A. G. C. A Outra Dimensão da Dimensão Fractal. Ciência Hoje. 183, 2002, Vol. 21, p. 40.
Autor do Texto: Paulo Henrique Gonsalves