Por: Gabriele Chomen

            O estudo das ciências exatas vem sendo realizado, queira ou não, ainda de uma forma muito abstrata em sala de aula, onde vários conteúdos são abordados e desenvolvidos apenas teoricamente e com equações, não tendo sentido para os alunos e até mesmo alguns professores. Esse processo de ensino-aprendizagem vem reforçar as dificuldades que muitos encontram em compreender os conteúdos trabalhados nessa disciplina. Mas se encontrássemos exemplos e aplicações, das teóricas seria menos abstrato, não?! É por este motivo que hoje iremos definir parcialmente o que é uma parábola e daremos algumas aplicações dela.

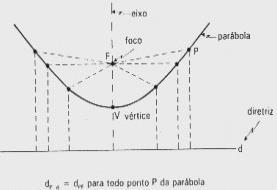
            Denominamos parábola ao lugar geométrico dos pontos de um plano que são equidistantes de uma reta dada d e de um ponto dado F, F ∉ d, do plano. O ponto F chama-se foco e a reta d chama-se diretriz da parábola. A distância entre F e d, que vamos representar por 2p, chama-se parâmetro da parábola. O ponto V da parábola, tal que dVF = p, é o vértice e a reta VF é denominada eixo da parábola (eixo de simetria da parábola).

           As aplicações da parábola, em 3D(paraboloide) são inúmeras, como:

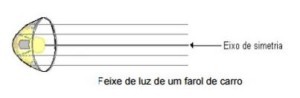
• Ao ligar faróis de carro, os raios de luz, provenientes da lâmpada que se encontra no foco da parábola, incidem num espelho parabólico e são refletidos paralelamente ao eixo de simetria.

• Em Odeillo no sul da França, onde a incidência de luz do Sol é intensa, foi construído um grande espelho côncavo, que é usado como “forno solar”. Como a distância do Sol à Terra é de cerca de 150 milhões de quilômetros, quando o feixe de luz solar nos atinge, seus raios já estão praticamente paralelos. Portanto, ao se refletirem no espelho do forno solar, os raios desse feixe convergem para seu foco, onde haverá uma grande concentração de energia, tanto luminosa quanto térmica. Assim, no foco do espelho há uma elevação de temperatura e, nesse ponto, é colocado o dispositivo que irá utilizar a energia concentrada. Se a distância focal do espelho for 10 m, esse dispositivo deverá ser colocado a 10 m do vértice do espelho, ficando assim, exatamente sobre o foco.

• As antenas parabólicas, apesar de não refletirem luz, são espelhos. Elas são construídas para refletir ondas de radiofrequências, que tem comprimento de onda muito maior do que o da luz, com valores que variam de algumas centenas de metros até o mínimo de cerca de 0,3 m. Para esses comprimentos de onda, quase todas as superfícies são espelhos, mesmo que sejam cheias de buracos, como uma tela de arame. Se as ondas eletromagnéticas emitidas por um satélite, atingirem a antena parabólica ocorrerá a reflexão desses raios a um ponto chamado foco da parábola, onde está um aparelho receptor que converterá as ondas eletromagnéticas em um sinal que a TV transformará em ondas, que serão os programas que passam e as pessoas assistem diariamente.

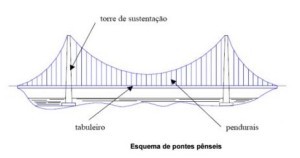
• As pontes pênseis ou suspensas são aquelas que possibilitam os maiores vãos. Nelas o tabuleiro contínuo é sustentado por vários cabos metálicos ligados a dois cabos maiores que, por sua vez, ligam-se às torres de sustentação. Os cabos comprimem as torres de sustentação, que transferem os esforços de compressão para as fundações. Nas pontes pênseis os tirantes são espaçados regularmente, então a carga da ponte é uniformemente distribuída nos cabos e estes formam uma parábola.

           Conclui-se que a  parábola é uma curva plana muito utilizada no dia-a-dia, embora na maioria das vezes passamos despercebido e não vemos que estamos utilizando dessa figura tão importante. Se mais exemplos fossem dados na sala de aula, talvez os alunos puderam observar mais a utilidade das parábolas, com grande surpresa! Se todos os conceitos fossem abordados desta forma os alunos não enfrentariam as aulas de exatas no ensino médio só para no fim falar: “Eu nunca irei usar isso mesmo!”.

            Referências; 

Ensino Fundamental: Função quadrática (Parábola). Disponível em: http://pessoal.sercomtel.com.br/matematica/fundam/eq2g/quadratica.htm. Acessado dia 08 de março

Parábolas. Disponivel em: http://www.rumoaoita.com/site/attachments/011_artigoconicascap3.pdf. Acessado dia 08 de março

 PAIVA, Manoel. Matemática. Vol. Ú. São Paulo. Editora Moderna, 1999.