Matheus Henry Przygocki
Qual é o caminho mais rápido entre dois pontos com uma aceleração constante? Não, não é uma reta.
Apesar de a resposta óbvia parecer ser uma reta, com as extremidades nos dois pontos, a reta é um dos caminhos menos eficientes em questão de velocidade. É o caminho mais curto, claro, mas não o caminho mais rápido, pois, a troca de energia potencial em energia cinética é muito lenta. O trajeto opitimo seria um equilíbrio nesta troca.
Este problema foi levantado em 1696 por Johann Bernoulli, um matemático que na época procurava estabelecer sua reputação científica. Então ele propôs este desafio aos estudiosos e estabeleceu um prazo de seis meses para publicação da resposta. Foram publicadas ao total, cinco soluções, a do próprio Johann, a de Leibniz, a de seu tio Jacob Bernoulli, a de L’hôpital e uma em anonimato, que mais tarde foi assumida por Newton.
A solução de Bernoulli, consiste em uma adaptação da lei de Snell, pois, como sabemos pelo princípio de Fermat, a luz sempre escolhe o trajeto mais rápido a percorrer. Pela lei de Snell, sabemos que quando a luz troca de meios onde sua velocidade varia, como o ar e a água, ela acabe assumindo um ângulo para melhor fazer uso do trajeto, com finalidade de sempre escolher o caminho mais rápido.
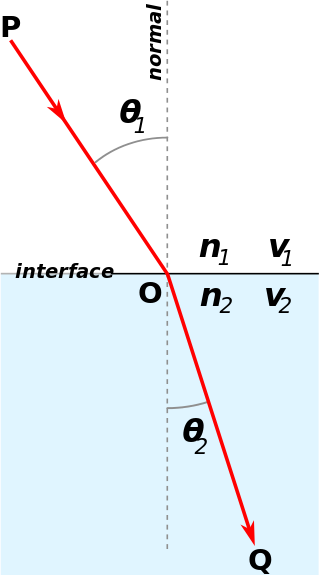
Bernoulli então, fez uma aproximação limite, onde existem infinitos meios de tamanho infinitesimal naquele meio, de modo que se torne uma mudança constante de trajetória.

O resultado implica um cicloide, que é a trajetória de um ponto em um polinômio ou circunferência em rolamento.
Este cicloide se provou como a solução do problema, pois é o trajeto que melhor administra a troca de energia potencial em energia cinética sem estender demais a trajetória.

Se não acredita em mim, veja o vídeo feito pelo canal Vsauce nas referencias abaixo:
Referencias:
“Cicloide”; Disponível em: <http://www.lem.xpg.com.br/Cicloide/cicloide.htm>; Acessado em: 03 de abril de 2017
“The Brachistochrone”; Disponível em: <https://youtu.be/skvnj67YGmw?t=17m57s>; Acessado em: 03 de abril de 2017.
